 |
 |
| d=0 | d=1 | d=2 | d=3 | d=4 | d=5 | |
| n=0 | 1 | |||||
| n=1 | 1 | 1 | ||||
| n=2 | 1 | 2 | 1 | |||
| n=3 | 1 | 3 | 3 | 1 | ||
| n=4 | 1 | 4 | 6 | 4 | 1 | |
| n=5 | 1 | 5 | 10 | 10 | 5 | 1 |
Above are coefficients of (a+b)^n for n= 0 to 5.
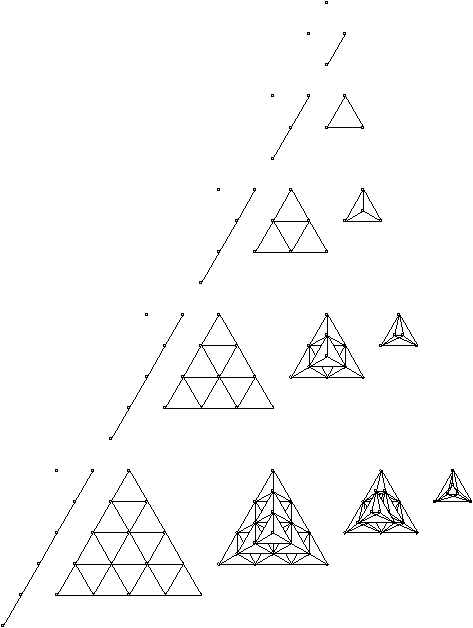
The two dimension simplex is the triangle. The numbers in the d=2 column
are triangle numbers.
Triangle numbers can be arranged in this way:
0
00
000
0000
They are sums of consecutive integers starting from 1.
Tetrahedron numbers are sums of consecutive triangle numbers starting
from 1.
I call the set of positive integers line numbers because they can be
arranged in a line.
The number sixteen, for example could be arranged thus: 0000000000000000
I think of one as the point number.
I believe the dth column of Pascal's triangle shows consecutive d-simplex
numbers.
This assumes a point is a 0 dimension simplex and a line segment is
a 1 dimension simplex.
Swarthmore
Math Forum's Pascal's Triangle Page
Sierpinksi
Pattern's in Pascal's Triangle