 |
|
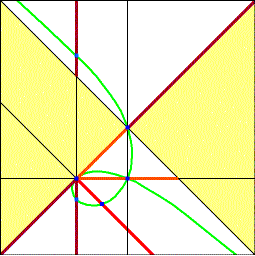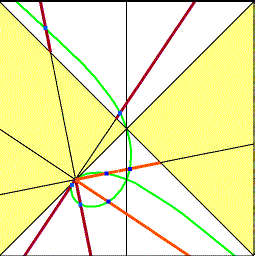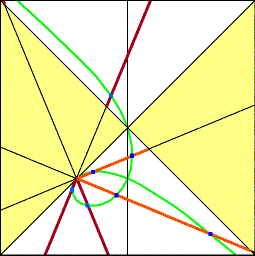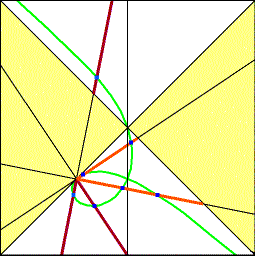
Parabola - Red Ellipse - Orange Blue Dots - Foci Green - Path of foci This curve is a strophoid. Thank you to Jean-Pierre Ehrmann of France for telling me this. |
 |
|
Parabola - Red Ellipse - Orange Blue Dots - Foci Green - Path of foci This curve is a strophoid. Thank you to Jean-Pierre Ehrmann of France for telling me this. |
|
- Clive Tooth followed Alexander's post with a demonstration using a Dandelin sphere: - Consider a cone. Let the vertex of the cone be V and let g be a generator. Call the axis of the cone x. Let A be a fixed point on g. Let B be the point on x which is closest to A. Let r be the line through A which is tangential to the cone and which is perpendicular to g. (r is not visible in this diagram because it's perpendicular to the screen) - Consider the pencil of planes through r. Let P be one of these planes. P will intersect our cone in some conic section. |
inscribed in the cone and touching P, at a point F. It is well known that F is a focus of our conic section. - Clearly C is on x and the points ABC and F are in the same plane. - 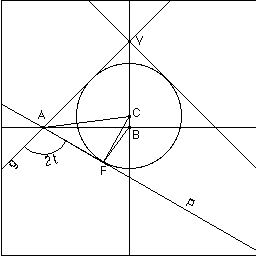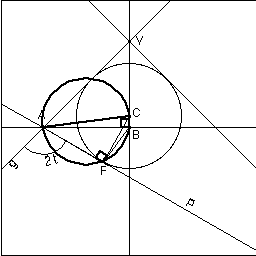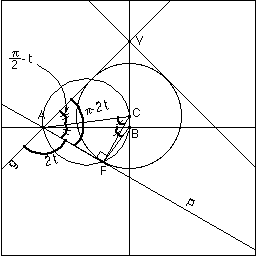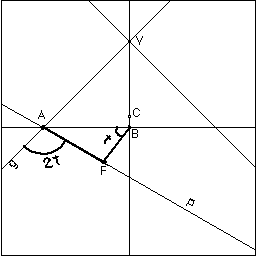 |
the angle that AF makes with g, on the side of P away from the sphere. Call this angle 2t. Now the angles CBA and CFA are both right angles. So the points ABC & F are concyclic. So the angle ACF is equal to the angle ABF. But the angle CAF is (pi-2t)/2 = pi/2 - t, so the angle ACF is t, so the angle ABF is t. - Thus, A and B are fixed points such that for any position of the plane P, the angle gAF is twice the angle ABF. - Thus, the point F is the intersection of two rotating lines (BF and AF) whose angular velocities are in the ratio 1:2. - QED |
 |
|
|