
|
| This perspective drawing utilizes the harmonic sequence. The heights of the rows are 1, 1/2, 1/3, 1/4, 1/5, etc. Crab print available here |

|
| This perspective drawing utilizes the harmonic sequence. The heights of the rows are 1, 1/2, 1/3, 1/4, 1/5, etc. Crab print available here |

|
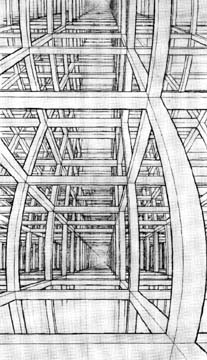
- Escher noted a flaw. A skyscraper viewed straight on from another skyscraper can be drawn the normal way. However, looking up or down at the skyscraper, the vertical lines aren't parallel. - Escher made wider angle perspective drawings that have several vanishing points. The vertical lines would gradually curve from parallel into converging. To the right are two such drawings: House of Stairs and a preliminary study for House of Stairs |
|

|
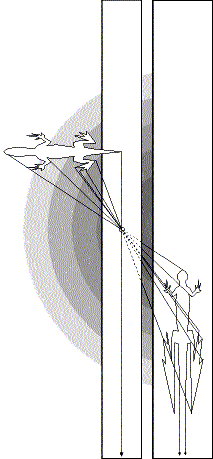
| - With this model you can go just a deep as you like into peripheral vision. Line segments running east and west become elongated as they approach the YZ plane where X=0. This distortion isn't visible to our eyes since our retinas are spherical, not planar. It also isn't noticeable in most pinhole camera photographs because the image goes off the edge of the photo paper before the distortion becomes obvious. - Imagine an infinitely large pinhole camera in 3D Cartesian space. The Y Axis runs north and south, the X Axis runs east and west, and the Z Axis up and down. The front of the camera is the YZ plane where X=0. The film plane is the YZ plane where X=-1 The pin hole is the origin. - The domain is all the points (x,y,z) such that x>0. The range is all points (x,y,z) such that x=-1 Points (x,y,z) in to the domain map into points (-1, -y/x, -z/x) in the range. |
|

|
| In the first one D=E, so A=B In the second, D=2E, So A=2B. Since A remains the same, B is half size. In the third D=3E. B is one third size, etc.. |
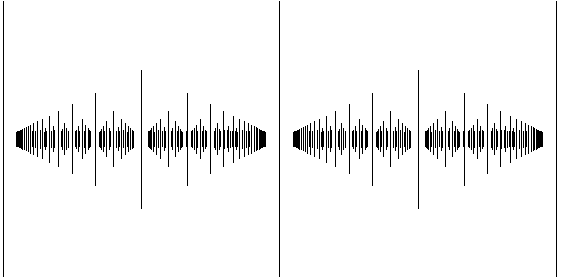
|
| There are 20 rows of poles. Thank you, Michael Carnright, for showing me this stuff. |

|
| - Alas, this is where the similarities end. The lines of a Poincare disk all meet the horizon at 90 degree angles. In my world, all lines running east to west converge at the eastern and western points of the horizon and intersect the horizon at every angle. - Along the north to south diameter in the disk above, the east to west lines intersect in a harmonic sequence. The east to west diameter is one radius from the horizon, the line above it, 1/2 r, 1/3 r, etc. - Anyway this is how the points map: (x, y) |--> (x/r, y/r) with r = sqrt( x^2+y^2)+1 - Sascha Rogmann gave me this equation which is much better than my initial effort. He also explained to me this disk is a nonconformal Euclidean space. Comparisons of Euclidean, hyperbolic (like the Poincaré disk) and elliptic spaces are at http://aleph0.clarku.edu/~djoyce/poincare/poincare.html - The vertical lines in this mapping curve in a way similar to Escher's house of stairs. I find it curious that Escher didn't bend the horizontal lines in the same fashion. - Dick Termes has an interesting essay on multi point perspective at http://termespheres.com/perspective.html |
