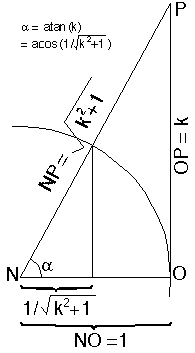
I've tipped over the triangle NOP, placing N at the center of a unit circle.
I hope this makes it more obvious that
alpha = atan(k) = acos(1/sqrt(k^2+1))

recall the expression for r coordinate of Q was
sin(alpha) cos(alpha) =
tan(alpha) cos^2(alpha) =
tan(atan(k)) cos^2(acos(1/sqrt(k^2+1))
k/(k^2+1) = 
1/(k+1/k)

Recall the z coordinate of Q was
sin^2(alpha) =
tan^2(alpha) cos^2(alpha) =
tan^2(atan(k)) cos^2(acos(1/sqrt(k^2+1))) =
k^2/(k^2+1)

So, as asserted before, Q's cylindrical coordinates
(sin(alpha) cos(alpha), phi, sin^2(alpha))
can be expressed as
(1/(k^2+1), phi, k^2/(1+k^2)


 

My thanks to Ron Winther, Kirk Bresniker and Axel Harvey from Sci.Math for helping me out with the trigonometry.

 Back