Set a sphere on a plane. Map P on the plane to Q on the sphere by drawing a line from the north pole to P. The line pierces the sphere at Q. This is a Riemann sphere.
Illustration 1

 
Sphere Spirals by M.C. Escher
©1999 Cordon Art B.V. - Baarn - Holland.
All rights reserved. Used with Permission.
Illustration 2
-


A logarithmic spiral mapped to a Riemann sphere
I believe Escher's sphere spirals are logarithmic spirals mapped onto a Riemann sphere.
Illustration 2.1

Turn Escher's Sphere Spirals upside down and it's still the same!
I'll try to show logarithmic spirals mapped onto a Riemann sphere have 180 degree symmetry.
-


Part of a logarithmic spiral.
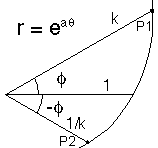Note that if r = k at angle phi, then r = 1/k at  - phi.
Illustration 3
-
Let phi be the angle from the x axis on the xy plane
At times I'll use cylindrical coordinates (r, phi, vertical distance),
and at times cartesian coordinates (r cos(phi), r sin(phi), vertical distance).
-
Line NP is directly above the OP. Therefore the xy plane angle Phi is unaltered by this mapping.
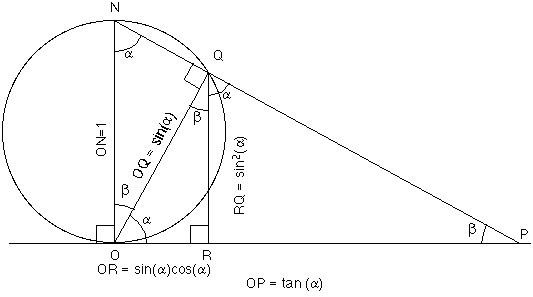
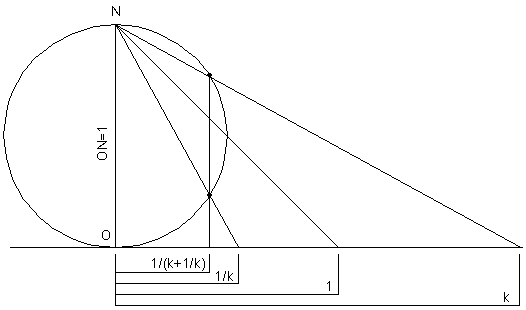
But the coordinates r and vertical distance are changed. 
Let the length of OP=k
-
Then alpha = atan(k) = acos(1/sqrt(k^2+1))
-
Cylindrical coordinates for Q are (sin(alpha) cos(alpha),    phi,    sin^2(alpha))
The trigonometric expressions can be given in terms of k. Explanation
(1/(k+1/k),    phi,     k^2/(1 + k^2))
-
Cartesian coordinates for Q:
((1/(k+1/k)) cos(phi), (1/(k+1/k)) sin(phi), k^2/(1+k^2))
Illustration 4

 
A point of cylindrical radius k maps into a point of radius 1/(k+1/k).
So points P whose radius = k or 1/k map into points with the same radius.
Illustration 5
-
Here's a rotation matrix for flipping objects 180 degrees around the x axis.
1
0
0
0
cos(pi)
sin(pi)
0
-sin(pi)
cos(pi)
-
In other words,
1
0
0
0
-1
0
0
0
-1
-
This is easy to compute:
(x i,   y j,   z k)
maps into
(x i,   - y j,   - z k)
Illustration 6
-
But I don't want to use the south pole as the pivot point,
I want to flip it around the point where the mapped spiral crosses the equator.
-
Recall the cartesian coordinates for Q are:
((1/(k+1/k)) cos(phi), (1/(k+1/k)) sin(phi), 1 - 1/(1+k^2))
-
I need to drop this sphere by 1/2 to get the equator on the x axis.
So subtracting 1/2 from the vertical coordinate:
((1/(k+1/k)) cos(phi), (1/(k+1/k)) sin(phi), (1 - 1/(1+k^2)-1/2))
-
 This simplifies to:
((1/(k+1/k)) cos(phi), (1/(k+1/k)) sin(phi), 1/2 - 1/(1+k^2))

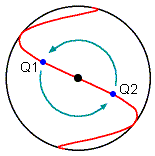
Recall points P1 and P2 in Illustration 3.
P1 cylindrical coordinates: (k, phi, 0)
P2 cylindrical coordinates: (1/k, -phi, 0)
-
Let P1 map to Q1    and    P2 to Q2 on our dropped sphere
-
P1, that is (k, phi, 0) ---> Q1, that is ((1/(k+1/k)) cos(phi), (1/(k+1/k)) sin(phi), 1/2 - 1/(1+k^2))
which can be rewritten:
((1/(k+1/k)) cos(phi), (1/(k+1/k)) sin(phi), (k^2-1)/2((1+k^2)))
-
P2, that is (1/k, -phi, 0) ---> Q2, that is ((1/(k+1/k)) cos(-phi), (1/(k+1/k)) sin(-phi), 1/2 - 1/(1+1/k^2))
which can be rewritten:
((1/(k+1/k)) cos(phi), -(1/(k+1/k)) sin(phi), -(k^2-1)/2((1+k^2)))
-

Note that that the rotation matrix of Illustration 6 maps Q1 to Q2 and vice versa.
Illustration 7

 
Escher's Drawing has four bands twisting around the sphere. Each band is bounded by two of the spirals described on this page. If the axis of rotation went through the band edge, the bands and empty space would be reversed.

Rather the axi through the equator should pierce the center of each band.

There are 4 more equatorial axi that pierce the centers of the 4 gaps that twist about the sphere.

I see 1 axes of 4 way symmetry going through the poles and 4 axes of 2 way symmetry going through the equator.
Illustration 8

-

Loxodrome Sphere
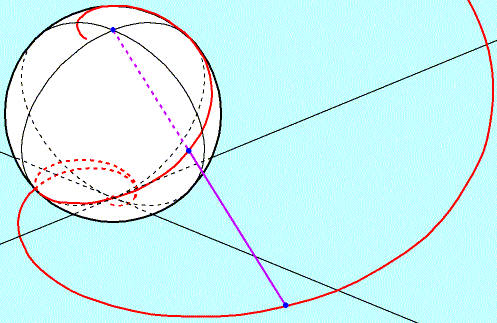
This is Ramiro Perez' image of a Loxodrome Sphere. Loxodromes intersect longitude lines at a constant angle. Logarithmic spirals cross radial lines through the origin at constant angles. The Riemann mapping is conformal (angles are preserved). Radial lines on the plane map to longitude lines on the Riemann sphere. These facts make me believe a mapping of a logarithmic spiral onto the Riemann Sphere is a loxodrome.


Back